이진트리:
노드가 왼쪽 자식과 오른쪽 자식만을 갖는 트리.
두 자식 가운데 하나 또는 둘 다 존재하지 않는 노드가 있어도 상관 없음.
이진트리의 특징은 왼쪽 자식과 오른쪽 자식을 구분한다는 점이다.
완전 이진 트리(Complete Binary Tree)
• 높이가 h이고 노드 수가 n개일 때
노드 위치가 포화 이진 트리에서의 노드 1번부터 n번까지의 위치와 완전히 일치하는 이진 트리
높이가 k인 완전 이진트리가 가질 수 있는 노드의 수는 최대 2^(k+1)-1 개 이므로, n개의 노드를 저장할 수 있는 완전 이진 트리의 높이는 log n 이다.
편향 이진 트리(Skewed Binary Tree)
• 높이가 h일 때 h+1개의 노드를 가지면서 모든 노드가 왼쪽이나 오른쪽 중 한 방향으로만 서브 트리를 가지고 있는 트리
순차 자료구조를 이용한 이진트리의 구현
1차원 배열의 순차 자료구조 사용
• 높이가 h인 포화 이진 트리의 노드 번호를 배열의 인덱스로 사용
• 인덱스 0번 : 실제로 사용하지 않고 비워둠 • 인덱스 1번 : 루트 저장
이진 트리의 1차원 배열에서의 인덱스 관계
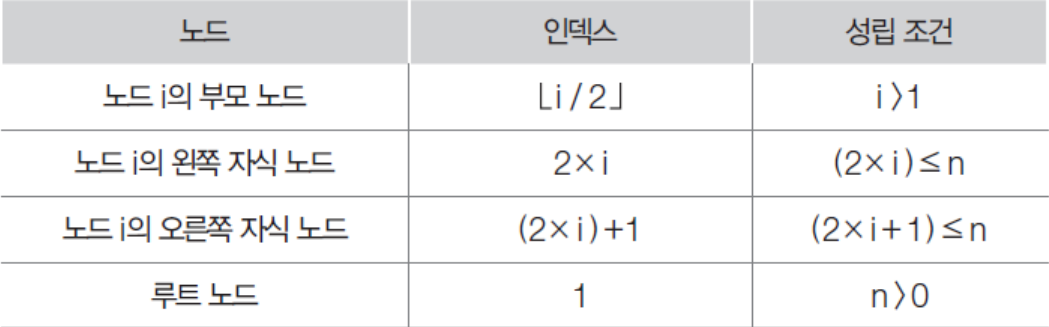
연결 자료구조를 이용한 이진트리의 구현
포인터를 사용하여 이진트리 구현
• 데이터를 저장하는 데이터 필드, 왼쪽 자식 노드를 연결하는 왼쪽 링크 필드, 오른쪽 자식 노드를 연결하는 오른쪽 링크 필드로 구성. 자식 노드가 없으면 링크 필드에 NULL을 저장하여 NULL 포인터로 설정
순서트리와 무순서 트리
형제노드와 순서 관계가 있는지에 따라 2종류로 분류된다.
순서관계 있으면 -> 순서트리
순서 관계 구별하지 않으면 -> 무순서 트리
순서 트리의 검색
순서 트리의 노드를 스캔하는 방법은 크게 2가지이다.
1. 너비 우선 검색
: 폭 우선 검색, 가로 검색, 수평 검색
낮은 레벨부터 왼쪽에서 오른쪽으로 검색하고, 한 레벨에서 검색을 마치면 다음 레벨로 넘어가는 방법
2. 깊이 우선 검색
: 세로검색, 수직 검색
리프에 도달할 때까지 아래쪽으로 내려가면서 검색하는 것을 우선으로 하는 방법이다.
리프에 도달해서 더 이상 검색할 곳이 없으면 일단 부모 노드로 돌아가고 그 뒤 다시 자식 노드로 내려감.
이진 검색 트리
모든 노드가 다음 조건을 만족해야 한다.
- 왼쪽 서브트리 노드의 키 값은 자신의 노드 키 값보다 작아야 한다.
- 오른쪽 서브트리 노드의 키 값은 자신의 노드 키값보다 커야 한다.
search()
1. 루트에 주목, 여기서 주목 노드를 p라고하자.
2. p가 None이면 검색 실패, 종료
3. 검색하는 key와 주목 노드의 p키를 비교
- key = p : 검색 성공, 종료
- key < p : 주목 노드를 왼쪽 자식 노드로 옮김
- key > p : 주목 노드를 오른쪽 자식 노드로 옮김
search()함수는 이와 같은 알고리즘을 바탕으로 이진 검색 트리에서 임의의 키를 갖는 노드를 검색한다.
키가 key인 노드를 검색하여 성공하면 찾은 노드의 값을 반환
add()
삽입할 때 주의할 점은, 노드를 삽입한 뒤에 트리의 형태가 이진 검색 트리의 조건을 유지해야한다는 점.
1. 루트에 주목, 여기서 주목 노드를 node라고 하자.
2. 삽입하는 key와 주목노드 node의 키를 비교.
- key = node인 경우: 삽입을 실패하고 종료.
- key < node 인 경우 :
- 왼쪽 자식 노드가 없으면 그 자리에 노드 삽입 , 종료
- 있으면 , 주목노드를 왼쪽 자식노드로 옮김
-key > node 인 경우 :
- 오른쪽 자식 노드가 없으면, 그 자리에 노드를 삽입하고 종료
- 오른쪽 자식 노드가 있으면, 주목 노드를 오른쪽 자식 노드로 옮김
remove()
노드를 삭제하는 과정은 삽입하는 과정보다 복잡하다. 노드를 삭제할때 다음과 같은 3가지 경우가 있기 때문이다.
A 자식노드가 없는 노드 삭제
B 자식노드가 1개인 노드 삭제
C 자식 노드가 2개인 노드 삭제
A 자식노드가 없는 노드 삭제 하는 경우
- 삭제할 노드가 부모의 왼쪽 자식이면, 부모의 왼쪽 포인터를 None으로 합니다.
- 삭제할 노드가 부모 노드의 오른쪽 자식이면, 부모의 오른쪽 포인터를 None으로 합니다.
B 자식 노드가 1개인 노드 삭제
- 삭제할 노드가 부모 노드의 왼쪽 자식: 부모의 왼쪽 포인터가 삭제할 노드의 자식을 가리키도록 업데이트
- 삭제할 노드가 부모 노드의 오른쪽 자식: 부모의 오른쪽 포인터가 삭제할 노드의 자식을 가리키도록 업데이트
(그니까 다음꺼를 그냥 이어주면 됨 빼려고 하는거 빼고)
C 자식 노드가 2개인 노드 삭제하는 경우
1. 삭제할 노드의 왼쪽 서브트리에서 키 값이 가장 큰 노드를 검색
2. 검색한 노드를 삭제 위치로 옮김, 즉 검색한 노드의 데이터를 삭제할 노드위치에 복사
3. 옮긴 노드 삭제. 이때 자식노드의 개수에 따라 다음수행
- 옮긴 노드에 자식이 없으면 :A
- 옮긴노드에 자식이 1개만 있으면 :B
작업을 한번씩 더 하는거네
모든 노드를 오름차순으로 출력하는 dump()함수
스캔은 중위순회의 깊이 우선 검색이래
'✍2021,2022 > 자료구조' 카테고리의 다른 글
| 자료구조 (0) | 2022.08.17 |
|---|---|
| 동적 계획법 (0) | 2022.08.08 |
| 큐 (0) | 2022.02.21 |
| 스택 (0) | 2022.02.16 |
| 자료구조(5) - 연결 자료구조와 연결리스트 (0) | 2022.02.09 |
